I am a Postdoctoral researcher in Applied Mathematics at FAU, Friedrich-Alexander-Universität, Erlangen (Germany), where I collaborate with Prof. E. Zuazua.
Before, I got a PhD in applied mathematics from the University of Bordeaux, (France) and I worked as a postdoctoral researcher at École Nationale des Ponts et Chaussées, Marne La Vallée, (France) with Prof. V. Ehrlacher.
Research interests
- Numerical methods for partial differential equations (especially model order reduction)
- Data-based/simulation-based methods, machine learning techniques
- Multi-physics coupled systems, domain decomposition
- Variational inequalities describing problems in contact mechanics, crowd motion
Some research activities
Multi-physics problems: component-based model order reduction
The application that motivated my doctoral thesis is the storage of high-level radioactive waste in geological media—I collaborated with Andra —the French National Agency for Radioactive Waste Management. The Thermo-Hydro-Mechanical (THM) equations model the behavior of temperature, interstitial water pressure, and solid displacement in the proximity of geological repositories, which contain radioactive waste and are responsible for a significant thermal flux toward the Earth’s surface. From a mathematical perspective, the THM system we solve is a coupled, time-dependent, and highly nonlinear system. Furthermore, the solution to the problem depends on several parameters, which may be related to the geometric configuration (e.g. the number of repositories, their distance, or their size) or to the material properties of the medium. Changes in the position and/or number of radioactive waste repositories could lead to significant variations in predicted quantities of interest; the need to solve the numerical model multiple times for design and assessment justifies the application of component-based parametric model order reduction (CB-pMOR). In Iollo et al. 2023 I proposed a CB-pMOR formulation for stationary problems in nonlinear elasticity. Finally, in Iollo et al. 2023 and in my PhD thesis I extended the CB formulation and methodology to time-dependent nonlinear problems with internal variables to solve the THM problem of interest.
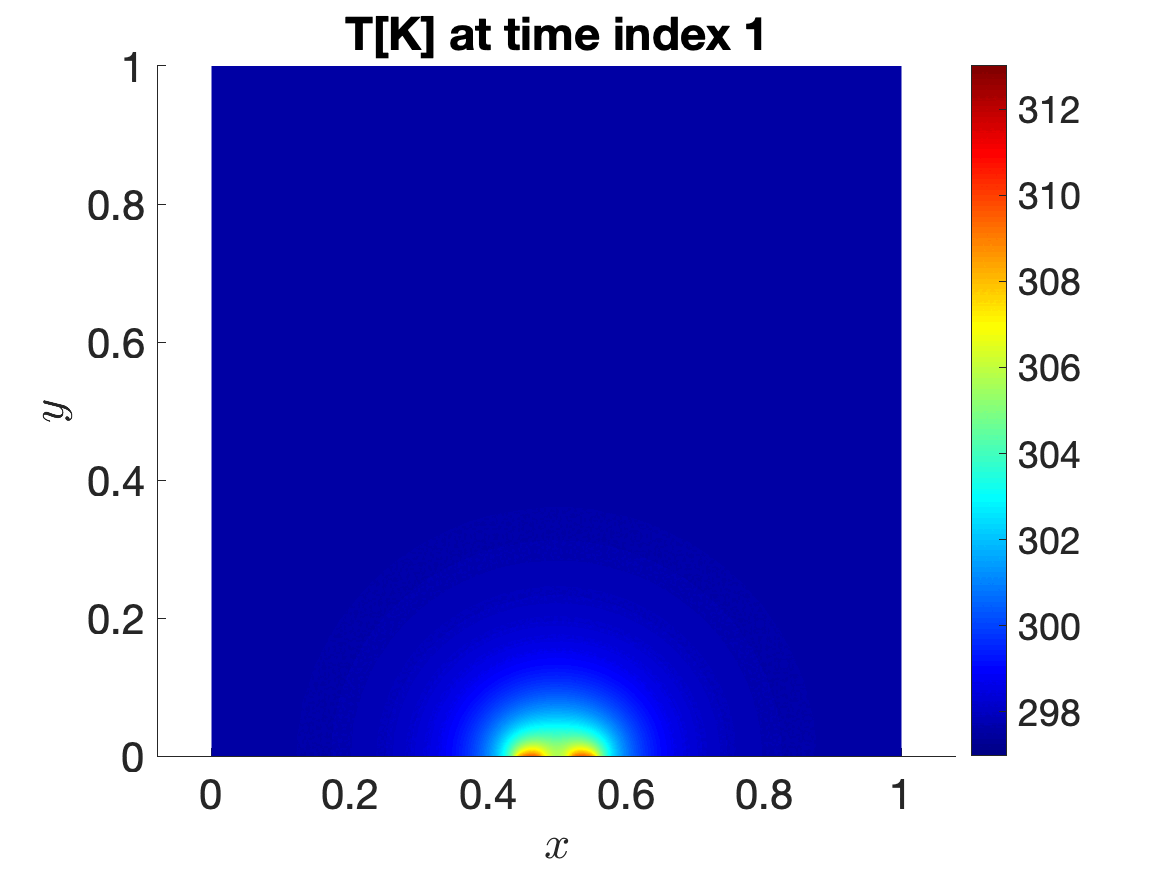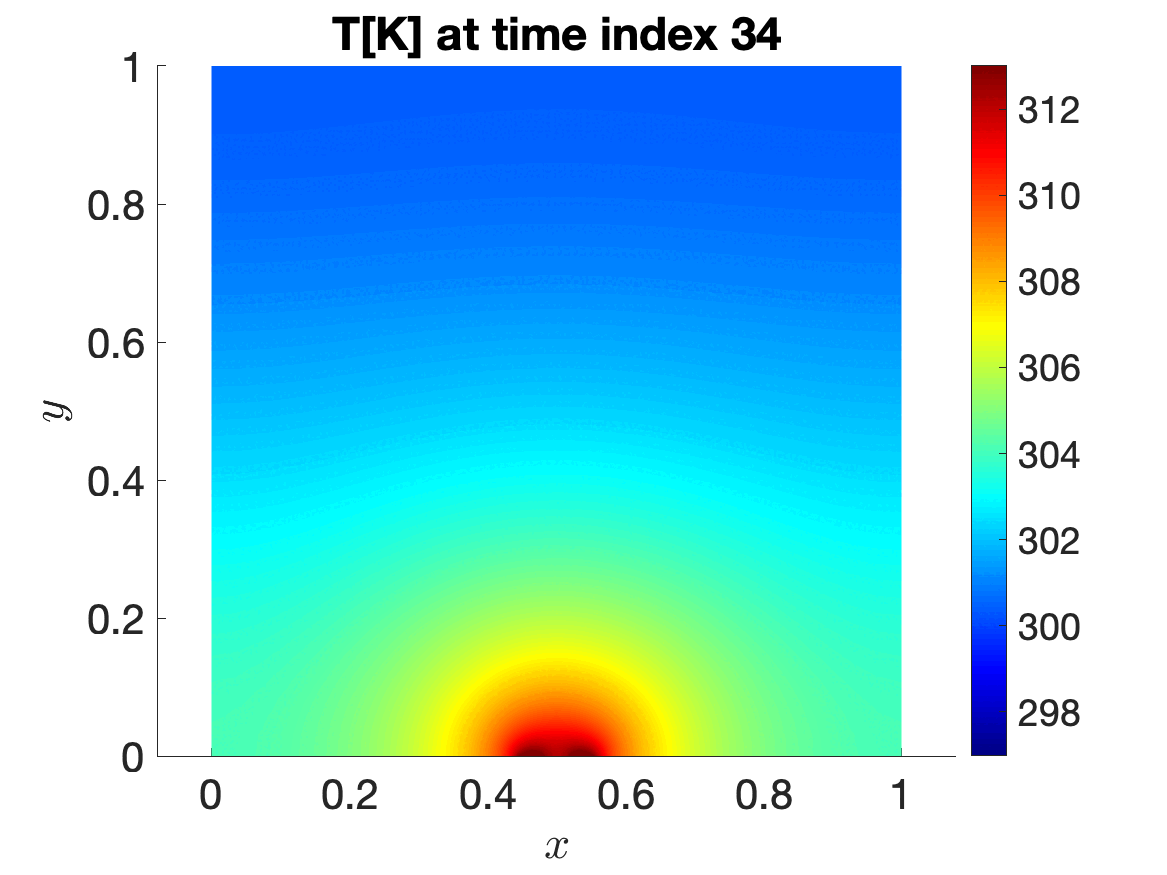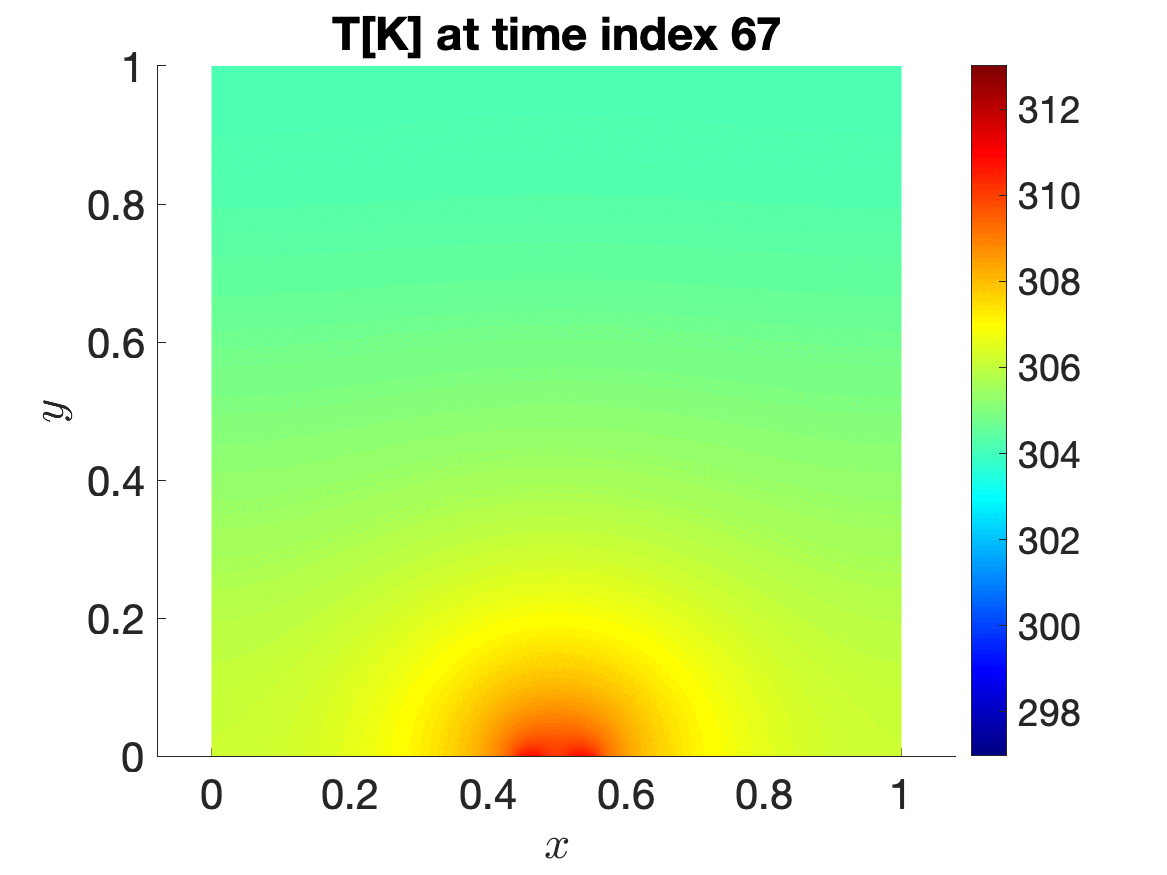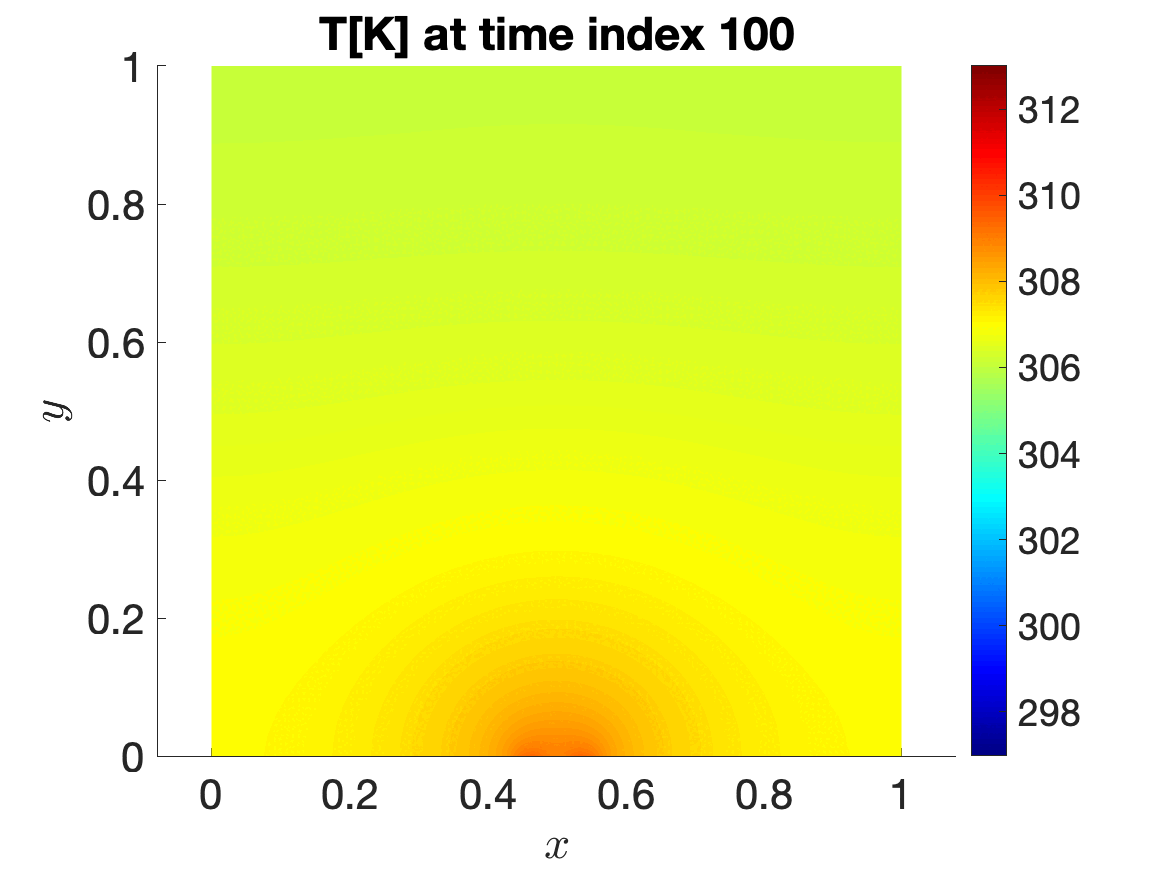
Time evolution of temperature T[K] for a 2-repositories configuration.
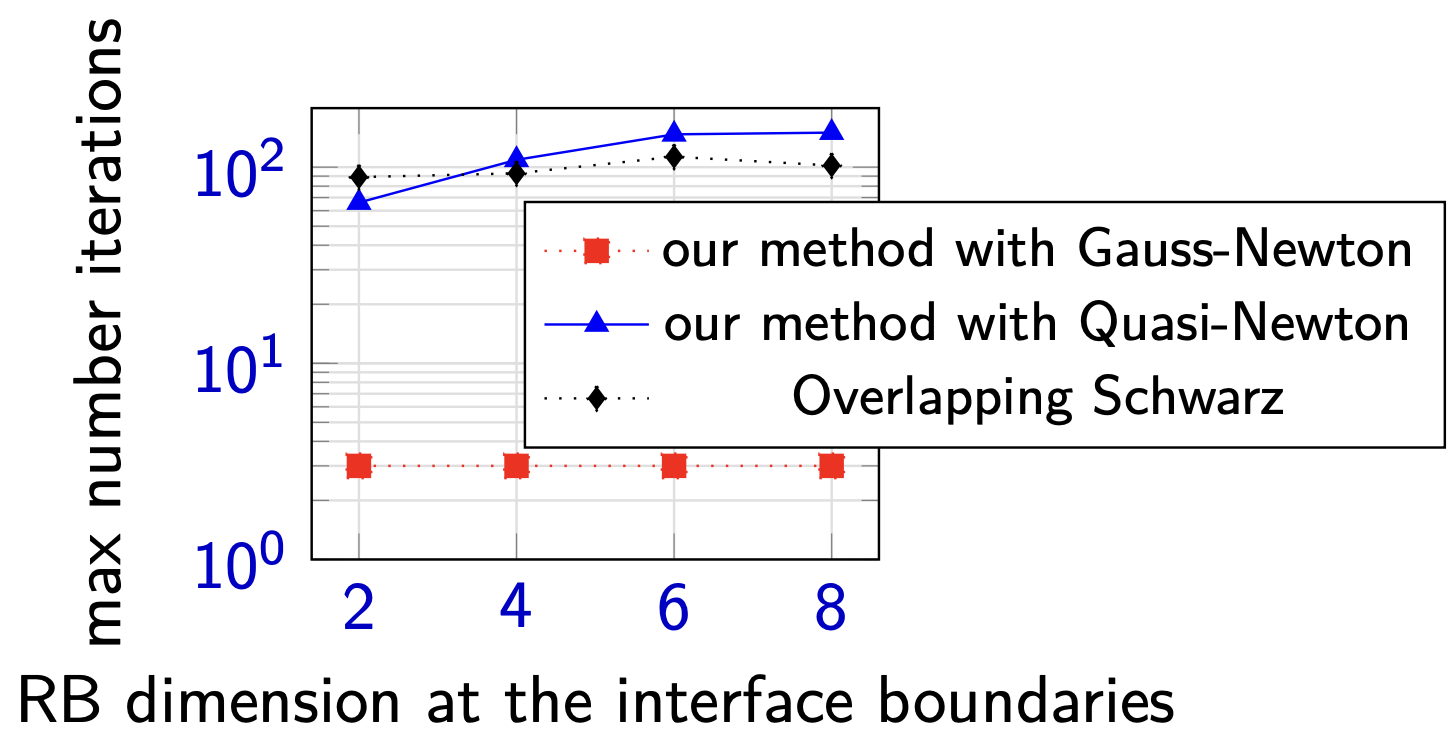
Our optimization-based method (red) with Gauss-Newton, quasi-Newton and the Overlapping Schwarz.
Multi-particles systems: model order reduction and machine learning.
During my postdoc, I adapted recent approaches in nonlinear model reduction to predict solutions for time-dependent, parameterized discrete contact problems: the model I adopted is a crowd motion in the presence of obstacles. I explored novel numerical approaches that combine the reduced-basis method with supervised machine learning techniques. In this pre-print I developed a hybrid method enabling more accurate and efficient predictions of particle velocities and contact forces compared to traditional methods.
